This is part 1 of 6 about learning the notes on the fretboard:
- Just 12 notes. (Background material — this page)
- Open and E strings
- Practicing with actual songs
- Fret 5 and String 5
- Octave Shapes
- Whole Fretboard
This section is purely background and doesn’t contain any exercises.
If you are in a rush and just want to start learning the fretboard, skip this page for now and proceed directly to learning the notes on the open and E strings. You can always return to this page later.
The goal is to get you on the path to learning, really learning all the natural notes on the fretboard. Unfortunately, this is a surprisingly steep early step to learning the instrument (and it really should be the very next thing you do after learning a few chords and strumming patterns).
Shapes versus Notes
A surprising number of guitarists never learn where all the notes are on the fretboard, much less how to read music. This is a real shame. Musicians learning almost any other instrument start by associating written notes on the staff with where and how to produce those notes on their instrument. It’s an odd quirk and unfortunate side-effect of a guitar’s layout that it’s common to start making music without ever learning the notes.
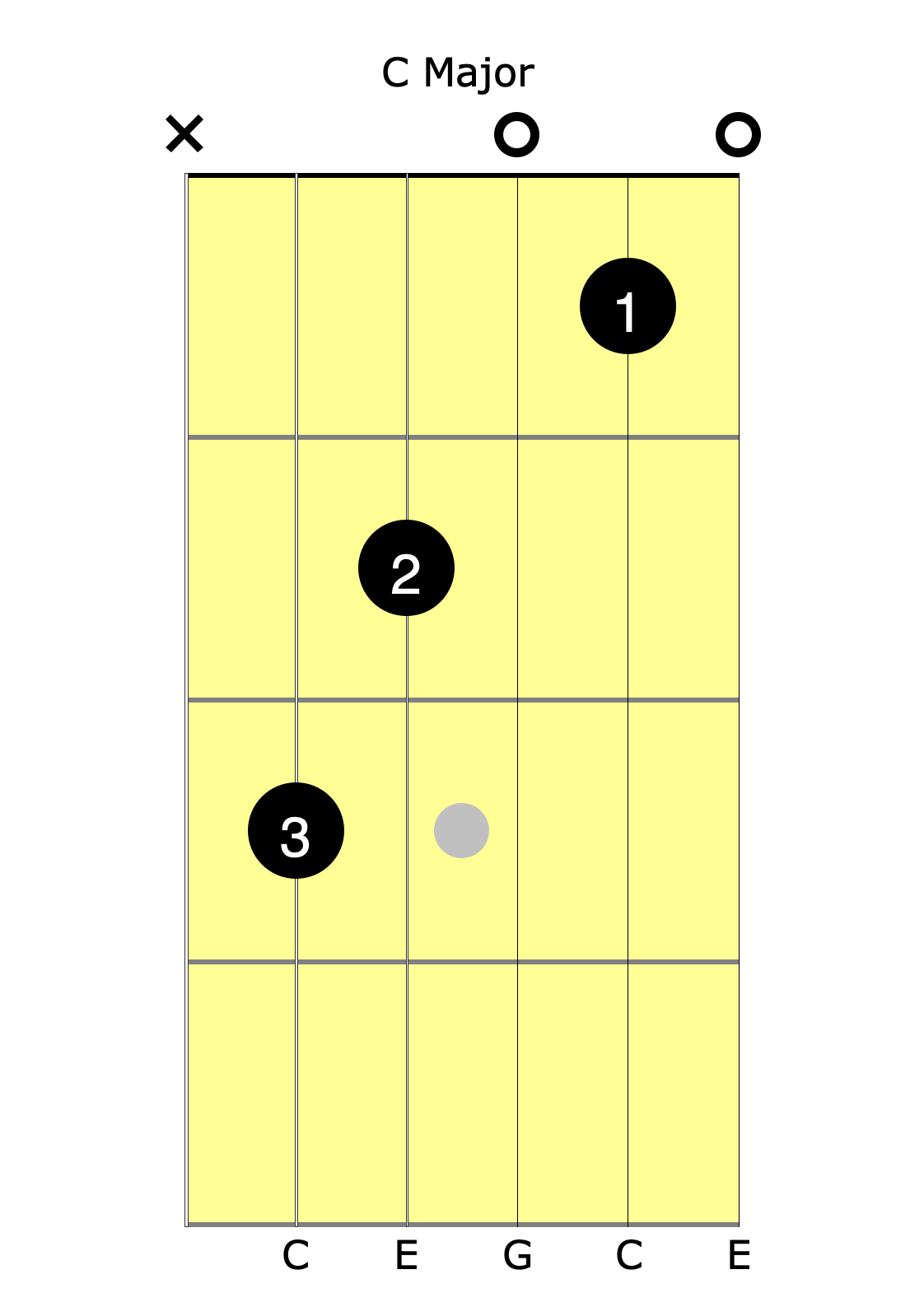
The guitar’s design encourages students to learn and think about fingering shapes rather than notes. To many guitarists, a C major chord is this shape (and only this shape!) up in open position:
But shapes aren’t music.
That diagram actually shows just one way to play the notes C, E, and G (the three notes in C major). From left to right starting on the 5th string, the diagram shows how to play the notes C, E, G, C (again), and E (again). It’s the three notes C, E, and G that make that a C chord, not the shape.
Seriously, even small children that have only been learning piano for a few weeks can play a C major in several ways all over the keyboard. Literally millions of guitarists, though, never learn any way other than the diagram above, which is just sad.
Music comprises just three things: rhythm, melody (individual notes spaced out in time), and harmony (notes played together). Notes are literally two-thirds of music.
Thinking in terms of fingering and shapes isn’t all bad. Shapes make it much, much easier to play in (or transpose to) different keys. This is something that can be quite difficult on other instruments. A guitarist is much more likely to play in a horn player’s natural key (like F or Bb) than for a horn player to play in E, A, D or G (convenient keys for the guitar).
But while shapes can be a useful device to help you memorize and find notes/scales/chords, you shouldn’t think of them as an end in themselves.
A few words about practicing
It will, unfortunately, take quite a bit of time (weeks to months) to become fluent at finding notes on the fretboard. But once you know (instantly and effortlessly) the name and location of every note on the fretboard the entire process of learning how to play the instrument gets easier.
Even just five minutes or so of daily practice will make the process pretty painless, but you just can’t escape several weeks or months of practice.
Don’t let “months” scare you: by the end of just the first day you should be able to instantly find any natural note (the notes A, B, C, D, E, F, and G) anywhere on the top or bottom strings. This means that by the end of day one, you’ll have likely memorized one third of the fretboard!
(The notes on the remaining four strings take so much more time because the effort is cumulative: each new note on each new string makes it progressively harder to remember what you’ve already learned.)
By the way: While learning the notes is a critically important first step, it isn’t necessary to put all the rest of your guitar practice on hold. I recommend putting in at least five or ten minutes during every single practice session drilling on note names until you’ve got it down, but it’s a very good idea to also study other things as you do so. Time spent learning songs, scales and arpeggios will also help to cement the note locations into your brain and fingers. Everything is interrelated.
It’s actually a mistake to overly force a “one step at a time” approach to learning the instrument, absolutely perfecting one thing before moving onto another. Learning music is like making a stew. A whole bunch of things need to simmer and steep before it starts making any kind of coherent sense. There’s little sense in becoming a world class carrot-chopper before you have at least a little experience making stew!
Why bother?
Why learn the notes on the fretboard? Several reasons, but chief among them:
-
It makes learning the instrument easier.
-
It indirectly improves your ear. Knowing which note is which makes it much easier to start hearing relationships between notes.
-
It makes it much easier to communicate with other musicians.
-
It makes learning music theory much, much easier. Learning theory in turn makes it easier to understand how songs are constructed, remember them, anticipate chords and melodies, and even to write your own.
-
Once you know the notes within any given chord, it makes it much easier to find chords all over the fretboard. As we saw, a C Major chord isn’t the shape you learned in open position when you first started (that’s just one way to play it). Once you can find the notes C, E, and G everywhere on the fretboard instantly and effortlessly, your rhythm guitar accompaniment will improve dramatically.
-
The same thing holds true with scales and modes. Learning the notes makes it much easier to solo and improvise. You’ll spend less mental effort as you make music.
-
It makes learning to read sheet music possible. I’m still ridiculously slow at reading, and learning to read on guitar is harder than many other instruments (because the same note can be played in so many different ways) but it’s not nearly as difficult as many guitarists would have you believe — if, that is, you don’t have to expend extra mental effort just locating notes!
KNOWING is more than knowing
Really knowing the location of a note someplace on the fretboard, by the way, means knowing it as well as you know letters of the alphabet, the names and colors of fruits, or names and nicknames of friends and family members.
It means: given a note name and a string, you can instantly, effortlessly find that note on the fretboard.
I call this KNOWING the note (all caps and bold).
KNOWING means that you can go the other way, too: if you plunk your finger down randomly anywhere on the fretboard, you want to be able to instantly, effortlessly name the note you landed on. Just like when you hear “green” you immediately visualize the color, and when see the color, your inner voice immediately names it.
It’s not enough to be able to indirectly work out the note by using interval shapes or counting up/down from another fret or string. KNOWING means you can directly recall without effort. You should almost see an imaginary note name floating above each fret location. Even the slight mental effort of figuring it out relative to something else you do KNOW will get in the way as you start doing more advanced things (like forming chords).
The musical alphabet
What follows is an over-simplified, highly condensed, and likely wrong history, but the concepts may prove helpful as we proceed. It attempts to answer some very common questions, including: Why are there 12 notes, but only 7 get a letter? Why do some notes have two names (like Eb/D#)? Why isn’t there a note called Cb or E#? Why is it called “diatonic”?
[This originated from a terrific comment I saw from the user “AlexrooXell” on reddit, by the way.]
In the earliest days of Western music (think Gregorian Chants) there were just seven notes. They were eventually named A, B, C, D, E, F, and G, but they could have been named John, Paul, George, Ringo, Larry, Moe, and Curly. They were just names.
Each note had its own pitch or tone, and each note in the sequence had a pitch that was higher than the prior one. The note B had a slightly higher pitch than A, and G was almost, but not quite, double the pitch of A.
Today, if you exactly double (or halve) the pitch of any given note, the resultant tone still keeps the same name. The tone produced at 440 Hz is called “A” but so are the tones at 880 Hz, 220 Hz, and 1760 Hz. They are all just the note “A”. (Look up “equal temperament” if you’re curious about why this wasn’t always true.)
It’s important to realize that the pitches between each of the seven notes were not equally spaced. The spacing was originally based on integer ratios like 3:2 and 5:4 that were pleasing to the ear. The resulting tones were roughly the same as those produced by the white keys on a piano today, including a smaller interval between B and C, and between E and F than between any of the other notes.
The seven notes produce successively higher pitches, and repeated indefinitely: A B C D E F G A B C D E F G A …. (This is why it’s called an “octave,” by the way — the sequence repeats at the eighth note.)
This uneven spacing of seven notes eventually became known as a “diatonic” scale. It was called “diatonic” (“two tones”) because the distance between any two consecutive notes was either a whole step (a “tone”) or a half step (a “semitone”). There were two types of tone intervals, hence “diatonic”.
Because of this uneven spacing, the sound/feeling of playing note sequences changes depending on which note you start from. This is particularly true when playing harmonies (two or more notes played at the same time) but is also true with melodies (individual notes played sequentially in time). Playing every other note starting from A sounds vaguely sad, but playing every other note starting on C sounds somewhat happy, for example.
If we start with C, there is a whole step to D, another whole step to E, a half step to F, whole steps from G to B, then another half step to begin another sequence starting with a higher C. This ordering of tone intervals (W W h W W W h) has a characteristic sound or feel that today we call “major” or “Ionian mode” if we’re feeling fancy. It has a vaguely happy sound.
If instead, we start with A, though, the intervals become W h W W h W W with a characteristic feel we call “minor” or “Aeolian mode”. Again, this sounds vaguely sad to most people.
If you start with G, you’re in “Mixolydian mode” (great for soloing over the blues today, but I’m unsure if any Gregorian blues survive).
The uneven spacing results in seven different “modes” for precisely the same collection of seven notes. It turns out that just by changing which note you start on (the “key”) you can make music with very different “feels” even though you’re using exactly the same notes.
Eventually, somebody thought: “But what if I want to produce (say) that sweet happy Major/Ionian sound, but starting with the note G instead of C?”
In other words, they wanted a group of seven notes that starts on G, but followed the W W h W W W h interval sequence of Ionian mode. It turns out that six of the original seven notes worked just fine, but one (F) was just wrong: G, whole-step to A, whole step to B, half step to C, whole step to D, whole step to E, but then we need a whole step to … what?
F is only a half step above E. G is too far (one and a half steps). They needed a note halfway between F and G for it to sound Ionian instead of Mixolydian. Since this tone replaces F in the sequence, but wasn’t F, they called it F#. It’s just another name, but for a new note that wasn’t used before.
It turns out that if you go through the process of creating every mode starting on each of the seven notes you end up needing five total of these “halfway” notes (between A/B, C/D, D/E, F/G, and G/A). Including the seven original “natural” notes, you end up with 12 uniquely named notes:
- A
- A# or Bb
- B
- C
- C# or Db (two names for the same note)
- D
- D# or Eb
- E
- F
- F# or Gb
- G
- G# or Ab
These “in between” notes have two names, which can be confusing. The rule is simple, though, just use the name based on what you’re replacing. In the example above, for G Ionian we replaced F so we called it F# and not Gb.
Here are the notes to create a major (Ionian) scale starting on each of the original seven notes:
-
A Ionian: A B C# D E F# G# (three sharps)
-
B Ionian: B C# D# E F# G# A# (five sharps)
-
C Ionian: C D E F G A B (no sharps or flats)
-
D Ionian: D E F# G A B C# (two sharps)
-
E Ionian: E F# G# A B C# D# (four sharps)
-
G Ionian: G A B C D E F# (one sharp)
For F Ionian, though, we start with F, whole step to G, whole step to A, and then we need a note between A and B. We’re replacing the note B, so this time we call it Bb, not A# (F Ionian: F G A Bb C D E).
- F Ionian: F G A Bb C D E
(You can also create major scales starting on the new “between” notes, but no further new notes are required.)
Anyway, the point is that we’ve ended up with 12 unique notes (and only 12 unique notes, even today). Seven of them are named A through G. These are the “natural” notes. The other five are “between” notes with two possible names depending on usage (the “sharps and flats”). Again, don’t get confused, these are just names.
We can start a scale “rooted” on any of these 12 notes, not just the seven natural notes (The Bb Major scale really is a thing, for example). Each of these 12 scales contains just seven notes, and seven different sounds (or modes) depending which of the seven notes you start on.
What’s in a name? Note names, scale degrees and intervals
The names of notes are absolute. They never change, no matter what scale, melody, or chord you’re playing. C is always called C. A D is always called D (and can always be found two frets higher than any C on the fretboard).
Confusingly, though, some notes have two “enharmonic” names (F# is also known as Gb, for example, but it’s the same note). Which we use depends on context (as described above). If we’re playing a song in the key of G major, we’d call the note F#. In the key of Db, we’d call it Gb. Either way, it’s the same note, and we’d never call it by any other name. Enharmonic names are a lot like nicknames: On legal documents you might see the name “Richard Starkey,” but in almost every other scenario you’d probably call him “Ringo.” It’s always the same guy, though, and we’d never call him “Paul” or “John.”
That’s the easy part.
That’s all you need to know to learn the notes on the fretboard: There are only 12 unique notes. A note’s name never changes, but it might have a nickname.
What follows confuses everyone when they first start studying music. It’s not necessary to learn the fretboard, but feel free to read through it and try to make sense of what you can. You may want to come back and re-read this material as you progress.
There are other ways to refer to notes that are relative to some other note, not absolute. These other names change depending on context (what the name is relative to).
One example of this are what are called scale degrees. Scale degrees are numbered relative to some note (known as the “root” of the scale). Scale degrees change depending on which note is considered the root of the scale.
The C Major scale, for example, comprises the seven notes C, D, E, F, G, A, and B in that order. C is the root note and 1st scale degree. D is the second scale degree, E the 3rd, etc. If someone says “play the flat five” they are telling you to play G♭ (“the 5” or the 5th scale degree, flattened by one semitone).
A scale is just a collection of notes. The collection of the seven natural notes (A, B, C, D, E, F, and G) has several different names as we’ve seen: C Major, A Minor, D Dorian, G Mixolydian, etc. Each of these scales (or modes) shares the same notes, and the names of those notes never change, but the scale degree of a given note does. G is the 5th scale degree of C Major, but the 7th scale degree of A minor.
Of these scales and modes using these seven notes, the major scale is by far the most important. Scale degrees are almost always named based on the major scale.
The other way of referring to notes is in terms of intervals. Intervals are always between pairs of notes. The interval from the note C up to the note D, for example, is called a Major 2nd.
Unfortunately, intervals can be confusing for at least a couple reasons:
-
The interval between the same two notes depends on which note is higher in pitch. C up to D (and D down to C) is a Major 2nd, but D up to the next higher C is a minor 7th.
Because notes can always be moved to different octaves without changing the character of the harmony, this can be particularly confusing. -
Some intervals have multiple names. Just as F# is also known as Gb, the interval from C to the note F#/Gb can be called an “augmented 4th” or a “diminished 5th” depending on context. To confuse you even further, that specific interval is also known as a “tritone” and is nicknamed “the blue note” as well as “the devils interval” (diabolus in musica).
Here is the name of each interval relative to, for example, C:
| Note Names | # Frets from C | Interval name(s) from C | Interval up to higher C |
|---|---|---|---|
| C | 0 | Unison | Octave |
| C#/Db | 1 | minor 2nd (m2) | Major 7th (M7) |
| D | 2 | Major 2nd (M2) | minor 7th (m7) |
| D#/Eb | 3 | minor 3rd/augmented 2nd (m3/+2) | Major 6th (M6) |
| E | 4 | Major 3rd (M3) | minor 6th (m6) |
| F | 5 | perfect 4th (p4) | perfect 5th (p5) |
| F#/Gb | 6 | augmented 4th/diminished 5th/tritone (+4/-5) | augmented 4th/diminished 5th/tritone (+4/-5) |
| G | 7 | perfect 5th (p5) | perfect 4th (p4) |
| G#/Ab | 8 | minor 6th/augmented 5th (m6/+5) | Major 3rd (M3) |
| A | 9 | Major 6th (M6) | minor 3rd/augmented 2nd (m3/+2) |
| A#/Bb | 10 | minor 7th/augmented 6th (m7/+6) | Major 2nd (M2) |
| B | 11 | Major 7th | minor 2nd (m2) |
| C | 12 | Octave | Unison |
Notes:
-
You can mostly ignore the last column in that table, but it’s worth knowing that the minor/major “character” of an interval flips when going up to the next higher root. It’s also worthwhile to know the numbers always add up to 9 (e.g. minor 3rd / Major 6th depending on direction).
-
The exceptions are the “perfect” intervals, the 4th and 5th. They are neither major nor minor, no matter which direction you go.
-
Perfect intervals can be diminished by flattening a half step, but flattening a Major interval makes it minor, not diminished.
-
Sharpening a minor interval makes it major.
-
Sharpening Major or Perfect intervals make them augmented.
-
[As an aside, F#/Gb is exactly halfway between Cs in two different octaves. It’s the only interval that stays the same whether you coming up from a lower C, or going up to a higher one.]
Finally, the last piece of complexity is that chord “extensions” use scale degrees that continue into the next octave.
To net it out, here are the various names of the natural notes in the C Major scale that we are learning:
| Note | Scale Degree | Steps from root | Interval from C |
|---|---|---|---|
| C (root) | 1 | 0 | Unison |
| D | 2 | W = 2 | M2 |
| E | 3 | WW = 4 | M3 |
| F | 4 | WWh = 5 | p4 |
| G | 5 | WWhW = 7 | p5 |
| A | 6 | WWhWW = 9 | M6 |
| B | 7 | WWhWWW = 11 | M7 |
| C* | 8 | 12 | Octave |
| D* | 9 | 12 + W = 14 | Major Ninth |
| F* | 11 | 12 + WW = 16 | Major Eleventh |
| A* | 13 | 12 + WWhWW = 21 | Major Thirteenth |
Notes:
-
In practice, you won’t always think about steps up from the root, even though you’ll likely use the name from the table when naming it out loud. You might say “B is the Major 7 in the C Major scale,” for example, but when you go to play it, it’s a whole lot easier to find “down a half step from C” than “up 11 frets from C”.
Similarly, you’ll just KNOW that the Major 6th is a minor third below the root, but you’ll still call it the Major 6th. In other words, you’ll likely think “relative from below” for degrees 1-5, and relative from above for degrees 6 and 7. Nobody thinks “up 14 half steps” to find the 9th! (Just “two frets above the root.") -
Extensions (beyond the first octave) are marked with an asterisk. Piano players usually keep the extensions in a higher octave, but guitarists often move notes to any octave. They may think of D’s in a lower octave as “ninths,” for example, because of fingering restrictions.
-
We create chords by “stacking thirds” (taking every other note). CMaj contains the notes C E G. CMaj7 = C E G B. CMaj9 = C E G B D. CMaj11 = C E G B D F (in theory). CMaj13 = C E G B D F A (in theory — that’s all the notes in the scale!). The reason there are no 10/12/14 scale degrees is because those notes are already present in the underlying, non-extended chords. You wouldn’t call an E in a higher register a “10th,” it’s still a Major 3rd relative to C, no matter what octave its in.
So if, for example, you were playing a song in the key of C Major, you could refer to the note E as the “3 note of the scale,” or “the major 3rd.".
One final source of much confusion: the chords associated with a scale also have numbers and major/minor/diminished/augmented tonality.
C Major contains the notes C D E F G A B but it also contains seven basic chords (or “triads”). By starting note in the scale in turn, we form the basic “triad” by taking every other note. So the “diatonic” chords in C Major are:
| Chord name | Roman or “Nashville” notation | Notes |
|---|---|---|
| C | I | C E G |
| Dm | ii | D F A |
| Em | iii | E G B |
| F | IV | F A C |
| G | V | G B D |
| Am | vi | A C E |
| Bdim | vii° | B D F |
So the chord F (Major) for example, is called the IV chord, and the note F is the 4th degree of the scale.
By convention, we use upper case roman numerals (I, IV, etc.) for major chords, lower case roman numerals (ii, vi) for minor chords, and Arabic numerals (1, 3, 5, etc.) for notes/intervals/scale-degrees. This helps considerably in written material, but it can be amazingly difficult to hear the difference in spoken words! It’s up to you to figure out if people are talking about chords or notes.
Totally made up band discussion:
Guitar: I really like the sound of a minor 9th on the “two” (ii) chord here. (Translation: adding the note E to Dm sounds cool.)
Bass: You want me to hit the 9? (Translation: Shall I play an E?)
Guitar: Nah, I’ll put it on top. Groove on the minor three. (Translation: Emphasize the note F instead.)
Drummer: You’re both rushing, tighten up. (Translation: I’m ready for a beer.)
Believe it or not, all of this will eventually become second nature.
We really only need to learn seven notes, not 12
Eventually, we want to KNOW the locations for all 12 notes, everywhere on the fretboard. What makes it difficult is that the guitar can produce the same note in multiple locations (On my 24 fret electric guitar, for example, I can play an E in thirteen different locations!!).
Fortunately, it’s enough just to learn the locations of the seven natural notes. The “between” notes (the “sharps and flats”) will always be one fret lower or higher. If you know where to find the note F, for example, and someone asks you to play an F#, you’ll find an F and just move your finger one fret higher.
This isn’t really KNOWING the location, but in practice a one fret move relative to another note you truly KNOW doesn’t require too much mental effort, and can be done in time, even at fast tempos!.
This concludes the background material. Let’s get on with actually learning the notes!