This is part 3 of a multipart series on triads:
- Triad introduction and triads on G/B/E
- Major triads on other strings using octave drops
- Harmonizing scales with triads (this page)
You now know all the close-voiced major and minor triad shapes on every string set, and all the major, minor, diminished, and augmented triads on the 1st string set (G/B/E strings).
Before moving onto the next session of practicing (and applying) triads across all the string sets, let’s spend some time harmonizing the major and minor scales on just the first string set.
As we discussed in just twelve notes, the major scale (AKA Ionian Mode) comprises just the seven natural notes C, D, E, F, G, A, and B.
We can create a triad for each of these notes by “stacking thirds” (playing every other note in the scale). We create a C triad from the notes C, E, and G (skipping over D and F). The next triad starts on D, and takes the notes D, F, and A, forming the D minor triad. The process repeats for all seven notes in the scale.
Here’s the table of these triads (chords) again:
| Scale degree | Chord | Roman or “Nashville” notation | Notes/spelling |
|---|---|---|---|
| 1 | C | I | C E G |
| 2 | Dm | ii | D F A |
| 3 | Em | iii | E G B |
| 4 | F | IV | F A C |
| 5 | G | V | G B D |
| 6 | Am | vi | A C E |
| 7 | Bdim | vii° | B D F |
Notice that the I, IV, and V chords are major, and the ii, iii, and vi chords are minor. The only oddball is the triad formed by starting on the seventh degree of the scale (B diminished).
To “harmonize” a scale just means to play the corresponding chord for each note in the scale (each scale degree). The harmonized C Major scale is the chords C, Dm, Em, F, G, Am, and Bdim.
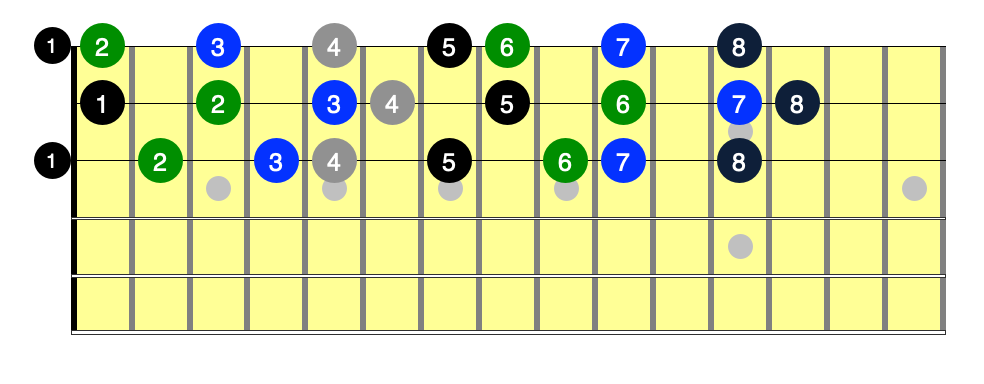
Here is the harmonized C Major scale on the top three strings using 2nd inversion triad shapes (with the 3rd in the bass):
This diagram starts with C Major (the black notes labeled “1” in the diagram). Then comes a Dm triad in green, then Em (blue), F, G, Am, Bdim, and finally back to C.
There are, of course, two more ways to harmonize the scale on this string-set, simply by starting with one of the other inversions of the C Major triad.
Any or all of those chords can be used to play songs in the key of C Major.
Harmonizing Melodies
You can harmonize melodies within a key using the harmonized triads. The song “Happy birthday to you” is usually played in the key of C. The first line of the melody is the notes C, C, D, C, F, E. You could harmonize this simply by playing the chords C, C, Dm, C, F, Em.
It might sound better, though, to keep the melody in the top “voice” and use different inversions of various chords within the key. You might play it this way, for example:
C (1st inversion with C on top)
C (1st inversion with C on top)
Dm (2nd inversion with D on top)
F (root inversion with C on top)
F (2nd inversion with F on top)
C (2nd inversion with E on top)
Other keys
The key of G Major contains the notes G A B C D E F♯. Only one note (F♯) differs from C Major. The chords are as follows:
| Chord name | Roman or “Nashville” notation | Notes |
|---|---|---|
| G | I | G B D |
| Am | ii | A C E |
| Bm | iii | B D F♯ |
| C | IV | C E G |
| D | V | D F♯ A |
| Em | vi | E G B |
| F♯dim | vii° | F♯ A C |
Even with only one note changed, the chords change significantly. The B chord is now Bm instead of Bdim. D is now major, not minor. And we play F♯dim instead of F major!
But, notice that the I, IV, and V chords are still major. The ii, iii, and vi chord still minor, and the vii° chord is still diminished. This remains true for any major scale, no matter how many sharps and flats.
The key of G♭ Major, for example, contains the notes G♭, A♭, B♭, C♭, D♭, E, and F♭. (Yes, we call it “C♭” here even though it’s really the same pitch and same note as plain old B).
The chords in G♭ are G♭, A♭ minor, B♭ minor, C♭, D♭, Em, and F♭dim.
Now let’s practice playing harmonized scales on the top three strings.
Exercise 23: Harmonizing major scales on G/B/E
Let's start with the key of C. Play the 2nd inversion C Major triad on G/B/E. Then move the root note up two frets to D and form the corresponding triad (Dm). Move up two more frets and play Em. Then one fret to F, two to G, two to Am, two more to the B diminished shape, and finally back to the C Major triad at the 13th fret. Refer to the diagram above if necessary.
Be sure to practice descending as well as ascend the scale. Play the C up at the 13th fret and work your way back down to the one in open position.
Now let's try a different inversion. Play the root inversion C Major triad with the C on the G string at the 5th fret. Move the C up two frets and play Dm. Then Em, F, G, Am, Bdim, and C.
Whenever you move too far up the neck to play comfortably, shift the shape one octave (twelve frets) lower and continue from there.
Repeat with the 1st inversion C Major triad at the 8th fret.
Once you have harmonized the scale with all three inversions, try to visualize how the different shapes overlap. Pick two chords, say C and F. first play them with the same inversion by shifting up and down the neck. Then play the same C shape, but this time try to find a different inversion of F nearby, without having to move your hand along the neck. Repeat for the other two C shapes.
Now do it with C and G. Millions of songs use I-IV-V chord progressions (C-F-G in the key of G). Knowing how to find nearby IV and V chords will prove incredibly helpful the more you play.
After you become comfortable with the key of C, pick another key and play that harmonized scale using all three inversions. You can just pick a key at random or proceed through the cycle of fourths/fifths (it isn't necessary to practice all keys on every string-set, but it won't hurt!).
Other Progressions (Becker Triad Exercise)
In addition to simply playing the harmonized scale in order (which doesn’t sound particularly musical) you can, of course, play the diatonic triads in any given order. One particularly useful ordering is progressing through the scale in sixths. Here’s an awesome YouTube video of David Becker explaining the sequence (the exercise itself starts at 3’22” but I highly recommend watching the whole thing).
Sixths are interesting because each pair of triads differs by only one note. You either raise the 5th of the triad up to the next scale degree, or lower the root.
C major is the notes CEG. Raising the G to an A gives you CEA (Am, 2nd inversion). Lowering the root gives you BEG (Em, 1st inversion). The process works with every diatonic triad: raising the fifth or lowering the root gives you another diatonic triad a sixth away.
I’m still unpacking all the ideas in that video myself. It’s a bit of a mental struggle the first few times, but the more I work on it, the more convinced I become that this exercise is money.
Exercise 24: Becker triads. Harmonizing in 6ths
Play the lowest C major triad on G/B/E (second inversion in open position). Raise the 5th to play Am. Now raise the 5th of the Am and play F. Then Dm, Bdim, G, Em, and then root position C.
You are simply raising the 5th to the next scale degree each time. We are in the key of C, so the scale degrees are just the natural notes (which you already KNOW, right?).
Now continue up the neck. Raise the G on the 1st string to an A and play Am (1st inversion) at the 5th fret. Then comes F, Dm, Bdim, G, Em, and once again you end on C at the 8th fret (1st inversion).
Continuing, raise the G on the 2nd string this time to A, and play the Am triad. Then continue raising 5ths to play F, Dm, Bdim, G, Em, and finally end on the 2nd inversion C again at the 13th fret.
This will be difficult at first. Notice the pattern, though: first the note on the 1st string is raised, then the 2nd string, then the 3rd. 1-2-3, 1-2-3, 1-2-3 indefinitely.
Now descend through the sequence, this time lowering the root each time.
Chord function
The nice thing about the Becker exercise is that it forces you to see how the shapes connect, and which chords are “closest” in terms of shared notes. I suspect this is particularly helpful for “voice leading” (finding chord inversions).
It led me to a bit of an epiphany regarding chord function (tonic/dominant/sub-dominant). I always knew that Am was the “relative minor” of C, and that the key of Am shared all the same notes as C Major, so it made sense to me that both C and Am (the I and vi chords) were in the “tonic” family. Both sound like “home.”
I never understood why Em (the iii chord) was also considered in the tonic family, though. Now I know. Both Em and Am are very closely related to C. You only need to change one note to get to either triad.
I recently came across this terrific article about chord function. That article coupled with the Becker Triad exercise really helped me learn something that I only vaguely understood before.
C to G is an interval of a fifth. The G triad functions as a dominant (C is the tonic, of course). F to C is also an interval of a fifth (C to F is a fourth) which is why it’s called the sub-dominant. Both share a note with the C triad. Playing a cadence of G Major to C Major gives a strong sense of resolution. Playing F Major to C Major also resolves, but not quite as strongly.
G is closely related to Bdim (only one note changes). Similarly, F is closely related to Dm (again, just one note differs). Both Bdim and Dm are utterly dissimilar to C. They share no common notes. C is spelled CEG, Bdim is BDF, and Dm is DFA. Bdim and Dm are as far from the tonic as you can get. Both G and Bdim perform the dominant function, and both F and Dm are sub-dominants.
To summarize:
| Function/Family | Chords | comments |
|---|---|---|
| Tonic | I, iii, vi | iii and vi share two notes with the I |
| Dominant | V, vii° | V & vii° share two notes, both share 0 or 1 note with the I |
| Sub-dominant | IV, ii | IV & ii share two notes, both share 0 or 1 note with the I |